Algebra 10: Week 2

1. Lesson 1: Trigonometry cont.

1. Вывести сумму углов
2. Примеры
3. Задачи
4. Үй тапшырмасы

1.1. Кошумча формула

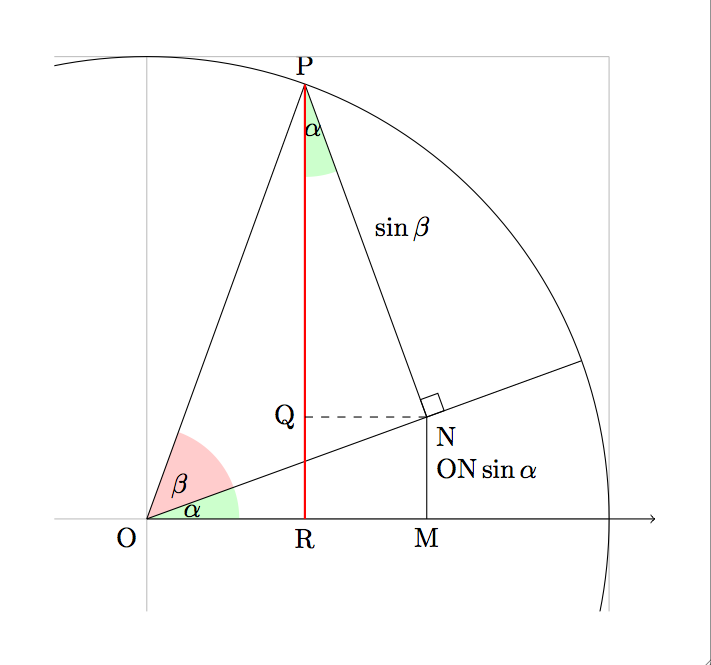
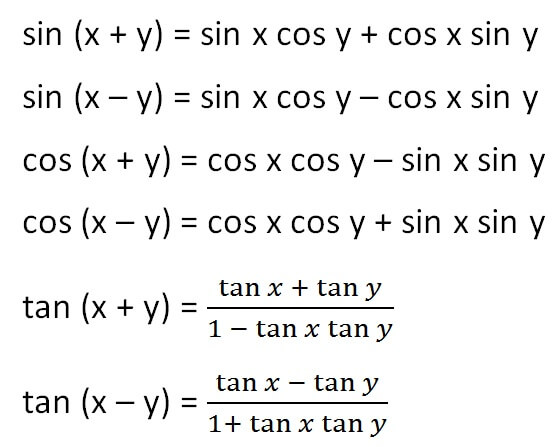
### Тема 3: Кошуу формулалары

1. Маселе: sin(45∘+30∘) маанисин тапкыла.
   • Чечүү: Синустун кошуу формуласы колдонулат: sin(α+β)=sinαcosβ+cosαsinβ.
2. Маселе: cos(60∘+θ) ни cosθ жана sinθ аркылуу чыгарыңыз.
   • Чечүү: Косинустун кошуу формуласы колдонулат: cos(α+β)=cosαcosβ−sinαsinβ.

—

### Тема 4: Эки эсе бурч формулалары

1. Маселе: sin2α маанисин табыңыз, эгерде sinα=12 болсо.
   • Чечүү: Формуланы колдонуңуз sin2α=2sinαcosα.
2. Маселе: cos2α маанисин табыңыз, эгерде tanα=1 болсо.
   • Чечүү: Формуланы колдонуңуз cos2α=cos2α−sin2α жана тригонометриялык функциялардын байланышын колдонуңуз.

—

### Тема 5: Сумма жана айырма формулалары

1. Маселе: sin(75∘−30∘) маанисин табыңыз.
   • Чечүү: Синустун айырмасы үчүн формула колдонулат: sin(α−β)=sinαcosβ−cosαsinβ.
2. Маселе: tan(θ−45∘) ни tanθ аркылуу чыгарыңыз.
   • Чечүү: Тангенстин айырмасы үчүн формула колдонулат: tan(α−β)=tanα−tanβ1+tanαtanβ.

—

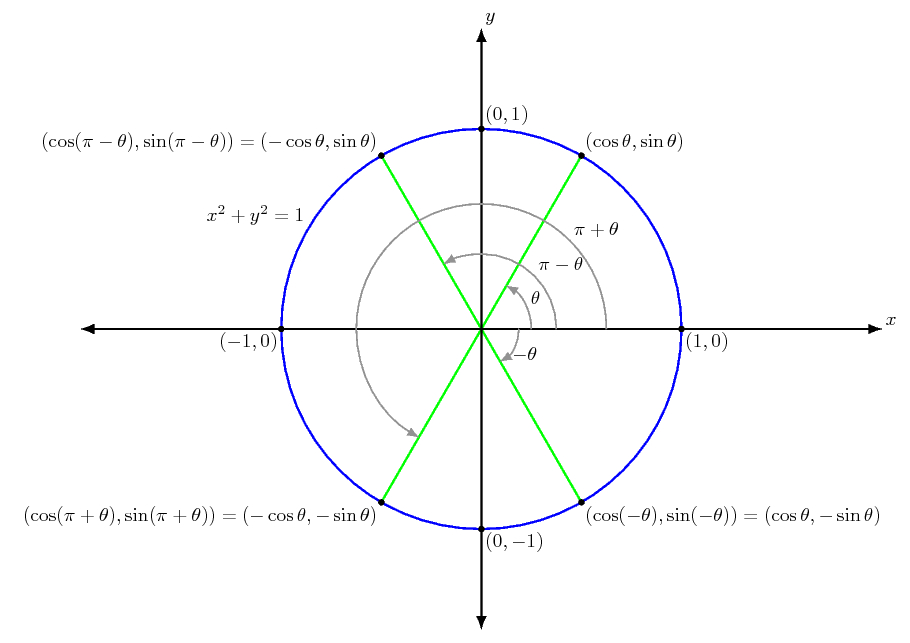
### Тема 6: Келтирүү формулалары

1. Маселе: sin(180∘−α) ни sinα аркылуу чыгарыңыз.
   • Чечүү: Келтирүү формуласы колдонулат: sin(180∘−α)=sinα.
2. Маселе: cos(90∘+α) маанисин sinα аркылуу чыгарыңыз.
   • Чечүү: Келтирүү формуласы колдонулат: cos(90∘+α)=−sinα.

—

### Тема 7: Тригонометриялык өрнөктөрдү жөнөкөйлөтүү

1. Маселе: 2sin2α+cos2α деген өрнөктү жөнөкөйлөтүңүз.
   • Чечүү: Косинустун эки эсе бурч формуласы жана негизги тригонометриялык теңдик колдонулат.
2. Маселе: 1−sin2αcos2α деген өрнөктү жөнөкөйлөтүңүз.
   • Чечүү: Эки эсе бурч формулалары жана тригонометриялык функциялардын байланышын колдонуңуз.

1.1.1. Сабактын жыйынтыгы (5 мүнөт)

1.1.2. Үй тапшырмасы

#### Тема 3: Кошуу формулалары

1. sin(30∘+45∘) жана cos(30∘+45∘) маанилерин кошуу формулалары аркылуу табыңыз.
2. cos(90∘−θ) ни sinθ аркылуу чыгарыңыз.

#### Тема 4: Эки эсе бурч формулалары

1. sin2α маанисин табыңыз, эгерде cosα=√32.
2. cos2α ни чыгарыңыз, эгерде sinα=35.

#### Тема 5: Сумма жана айырма формулалары

1. cos(60∘−45∘) маанисин айырма формуласы менен табыңыз.
2. tan(90∘−θ) ни тригонометриялык функциялар аркылуу чыгарыңыз.

#### Тема 6: Келтирүү формулалары

1. sin(270∘+α) ни sinα же cosα аркылуу чыгарыңыз.
2. cos(360∘−α) маанисин табыңыз.

#### Тема 7: Тригонометриялык өрнөктөрдү жөнөкөйлөтүү

1. sin(2α)⋅cos(2α) деген өрнөктү жөнөкөйлөтүңүз.
2. 1−2sin2α дегенди тригонометриялык теңдиктерди колдонуп жөнөкөйлөтүңүз.

Кошумча тапшырмалар:

• Эки эсе бурч формулаларын колдонуп, өз алдынча эки мисал түзүп, чечиңиз.
• sin2α=cosα деген теңдемени 0 градустан 180 градуска чейинки бурчтар үчүн чечиңиз.

1.1.3. Шилтемелер

• Desmos: Visual solution to equation

—

2. Сабак 2: Функциялар жана алардын графиктери

2.1. Үй тапшырмасы

Өз алдынча изилдеңиз
Функциялар. Аныкталуу областы жана маанилердин көптүгү. Функциянын графиги. Ар кандай жолдор менен берилген функциялардын графиктерин куруу. Функциялардын касиеттери: монотондуулугу, жуптугу жана тактыгы, мезгилдүүлүгү, чектүүлүгү

Функции и их графики. Свойства функций..Четность и нечетность. Периодичность тригонометрических функций. Возрастание и убывание Экстремумы. Исследование функций.