Algebra 10

Aidin Biibosunov

Created: 2024-09-09 Mon 19:55

1. Week 1

1.1. Lesson 2

1.1.1. Trigonometry

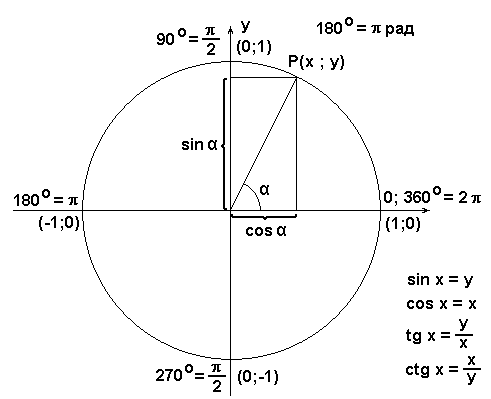
trig_circle.gif

### Тема 1: Определение и свойства синуса, косинуса, тангенса

  1. Задача: Найдите значения синуса, косинуса и тангенса для углов \(30^\circ\), \(45^\circ\), и \(60^\circ\).
    • Решение: Используйте определение тригонометрических функций для острых углов прямоугольного треугольника или единичной окружности.
  2. Задача: Даны значения \( \sin \alpha = \frac{3}{5} \). Найдите \( \cos \alpha \) и \( \tan \alpha \), если угол \( \alpha \) острый.
    • Решение: Используйте основное тригонометрическое тождество \( \sin^2 \alpha + \cos^2 \alpha = 1 \) и определение тангенса.

—

### Тема 2: Соотношение между тригонометрическими функциями одного угла

  1. Задача: Если \( \tan \alpha = 2 \), найдите \( \sin \alpha \) и \( \cos \alpha \).
    • Решение: Используйте соотношения \( \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \) и \( \sin^2 \alpha + \cos^2 \alpha = 1 \).
  2. Задача: Докажите, что для любого угла \( \alpha \) выполняется \( 1 + \tan^2 \alpha = \frac{1}{\cos^2 \alpha} \).
    • Решение: Воспользуйтесь основным тригонометрическим тождеством и выражением тангенса через синус и косинус.

—

trig_angles_sum.png

1.1.2. Функция (25m)

  • А: Объяснить что такое функция. Разные виды. Что ее можно представить графически. Общий вид линейной функции
  • И: https://www.desmos.com/calculator


  • Примеры из жизни Турмуштан мисалдар
    Тарифы на такси часто следуют линейной функции, где общая стоимость проезда рассчитывается как базовый тариф плюс ставка за километр. Это можно выразить как:
    Общая стоимость проезда = Базовый тариф + (Ставка за километр × Пройденные километры)

    Такси тарифтери көбүнчө сызыктуу функцияны аткарат, мында жалпы жол кире негизги тарифке плюс километрге эсептелген тариф катары эсептелет. Бул төмөнкүчө чагылдырууга болот: Жалпы жол кире = Негизги тариф + (Бир километрге тариф × Басылган километр)

    В линейной модели роста население: население увеличивается на фиксированное число особей каждый год. Это означает, что если население начинается с определенного числа, оно будет расти на ту же величину каждый последующий год. Например, если население города увеличивается на 100 человек в год (r=100), линейную функцию можно выразить как:
    Популяциянын өсүшүнүн сызыктуу моделинде: популяция жыл сайын жеке адамдардын белгиленген санына көбөйөт. Бул калктын белгилүү бир сандан башталса, кийинки жыл сайын ошол эле суммага өсөт дегенди билдирет. Мисалы, эгерде шаардын калкы жылына 100 адамга көбөйсө, анда сызыктуу функция төмөнкүчө чагылдырууга болот:

    \[P(t) = P_0 + rt \]

    Предсказание: Поскольку скорость изменения постоянна, это позволяет делать простые прогнозы. Например, если в 2020 году население города составляло 1000 человек и ежегодно увеличивается на 50 человек, то численность населения в 2025 году можно легко рассчитать следующим образом:
    \(P(5)=1000+(50×5)=1,250\)

У: Для функции \( y = 2x - 5 \):

  1. Найдите значения \( y \) при \( x = -1, 0, 3 \).
  2. Найдите значение \( x \), при котором \( y = 1 \).
  3. Постройте график функции.

Функция үчүн \( y = 2x - 5 \):

  1. \( x = -1, 0, 3 \) болгондо, \( y \) маанилерин табыңыз.
  2. \( y = 1 \) болгондо, \( x \) маанисин табыңыз.
  3. Функциянын графигин түзүңүз.

У: Придумать собственной пример где возникает линейная функция
Сызыктуу функция пайда болгон жерде өзүңүздүн мисал келтириңиз

1.1.3. Степень с целым показателем

Упростите выражения:

  1. \( (2a^3b^2)^2 \times (ab^{-1})^3 \)
  2. \( \frac{(x^4y^3)^2}{x^5y^6} \)

### 4. Многочлены

  1. Приведите подобные члены в выражении: \( 3x^2 - 5x + 7 + 4x^2 + 2x - 10 \).
  2. Найдите значение многочлена \( 2x^3 - 3x^2 + x - 5 \) при \( x = 2 \).

### 5. Формулы сокращенного умножения Разложите на множители:

  1. \( x^2 - 9 \)
  2. \( 4a^2 - 16b^2 \)

### 6. Уравнения с двумя неизвестными. Системы уравнений Решите систему уравнений:

  1. \[ \begin{cases} 2x + y = 7 \\ 3x - 2y = 4 \end{cases} \]
  2. \[ \begin{cases} x - 3y = 5 \\ 4x + y = -3 \end{cases} \]

### 7. Квадратные корни и действия с ними Упростите выражения:

  1. \( \sqrt{50} + 3\sqrt{2} \)
  2. \( \sqrt{45} - \sqrt{20} \)
  3. \( \sqrt{x^2 + 6x + 9} \)

1.2. Важно

  • Проверять ответы на здравый смысл